[알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) 구현(C++, Python)
카테고리: Algorithm Theory
태그: algorithm coding test dijkstra graph implementation graph
1. 🔍 다익스트라 알고리즘(Dijkstra Algorithm)
1959년 에츠허르 데이크스트라(Edsger Wybe Dijkstra)가 발표한 최단 경로를 구하는 알고리즘.
- 최단 경로(shortest path)는 그래프의 종류에 따라 다르게 해석된다.
- 가중치가 없는 그래프인 경우 간선의 개수가 가장 적은 경로가 최단 경로이지만 가중치가 있는 그래프에서는 일반적으로 거쳐가는 가중치의 총합이 최소가 되는 것을 말한다.
- 가중치가 있는 그래프의 최단 경로를 구하는 문제는 대부분 다익스트라 알고리즘을 사용한다고 보면 될 정도로 중요한 알고리즘이다.
2. 💡 다익스트라 알고리즘 동작 과정
- 시작 노드를 설정하고 시작 노드로부터 특정 노드까지의 최소 비용을 저장할 공간과 직전 노드를 저장할 공간을 마련한다.
- 최소 비용을 저장할 공간은 모두 매우 큰 값으로 초기화한다. 보통 무한대(infinite number)를 사용한다. 직전 노드를 저장할 공간도 무한대로 초기화한다.
- 시작 노드의 최소 비용은 0, 직전 노드는 자신으로 한다.
- 해당 노드를 통해 방문할 수 있는 노드 중, 즉 아직 방문하지 않은 노드 중 현재까지 구한 최소 비용이 가장 적은 노드를 선택한다.
- 해당 노드를 거쳐서 각 노드까지 가는 최소 비용과 현재까지 구한 최소 비용을 비교하여 작은 값을 각 노드의 최소 비용으로 갱신한다.
- 이때 직전 노드도 같이 갱신한다.
- 노드 개수에서 1을 뺀 만큼 반복한다.
3. ⚠️ 고려 사항
- 음의 가중치가 있는 그래프에서는 사용 불가능하다.
- 벨만-포드 알고리즘을 사용해서 풀 수 있다.
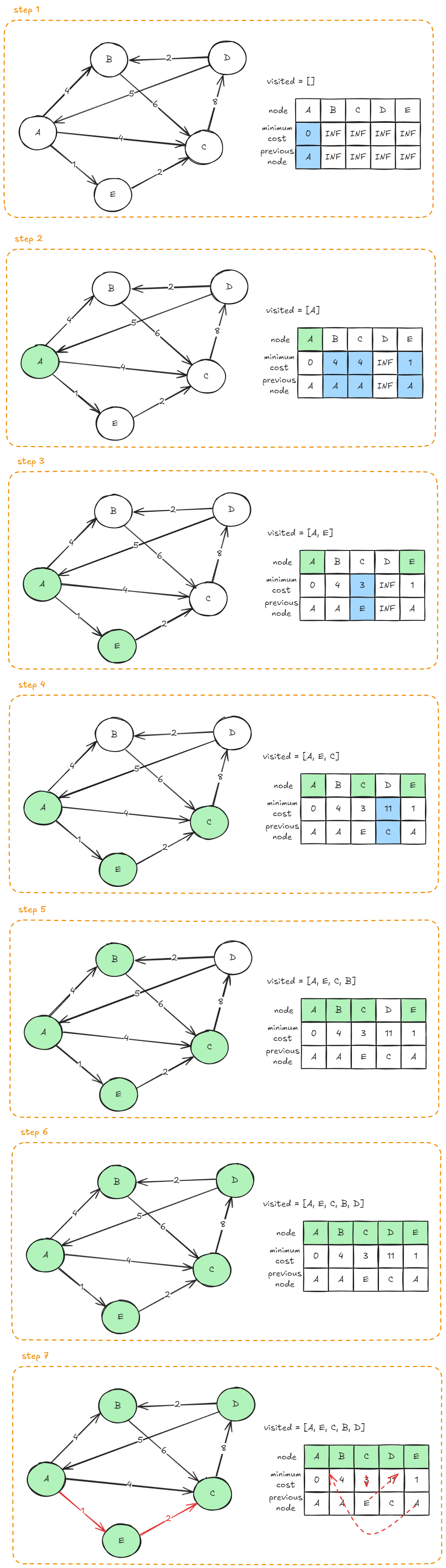
4. 🎨 그림과 함께 알고리즘 생각해보기
예시 그림과 함께 알고리즘을 생각해보자.
- 1단계: 시작 노드 A의 최소 비용은 0, 직전 노드는 A로 초기화
- 2단계: 방문하지 않은 노드 중 최소 비용이 가장 적은 노드 A를 선택한다. 이후 해당 노드를 거쳐서 각 노드까지 가는 비용과 기존에 구한 각 노드의 최소 비용을 비교한다. 노드 A에서 노드 B, C, E의 가중치는 각각 4, 4, 1이다. 현재까지 해당 노드의 최소 비용은 모두 INF이므로 각각 가중치로 최소 비용을 갱신한다. 이때 최소 비용이 갱신된 노드의 직전 노드를 A로 갱신한다.
- 3단계: 방문하지 않은 노드 중 최소 비용이 가장 적은 노드 E를 선택한다. 선택한 노드를 거쳤을 때 최소 비용을 갱신할 수 있는지 확인한다. 노드 C의 현재 최소 비용은 4이지만 E를 거쳐서 도달하면 1+2로 3이 될 수 있다. 현재까지 구한 최소 비용보다 이 값이 더 작으므로 C의 최소 비용을 3, 직전 노드를 E로 수정한다.
- 4단계: 방문하지 않은 노드 중 최소 비용이 가장 적은 노드 C를 선택한다. 선택한 노드를 거쳤을 때 최소 비용을 갱신할 수 있는지 확인한다. 노드 D의 경우 기존 최소 비용이 INF이지만 C를 거치면 3+8로 11이 될 수 있다. 최소 비용을 11로, 직전 노드를 C로 갱신한다.
- 5단계: 방문하지 않은 노드 중 최소 비용이 가장 적은 노드 B를 선택한다. 선택한 노드를 거쳤을 때 최소 비용을 갱신할 수 있는지 확인한다. 갱신 가능한 노드가 없음을 확인한다.
- 6단계: 방문하지 않은 노드 중 최소 비용이 가장 적은 노드 D를 방문한다. 마찬가지로 갱신 가능한 노드가 없다.
- 7단계: 모든 곳을 방문했다. 특정 노드로부터 직전 노드가 시작 노드가 될 때까지 거슬러 올라가면 최소 비용을 구성하는 세부 경로도 알 수 있다. 예를 들어 노드 C의 경우 최소 비용은 3이며, 직전 노드 E, A를 거슬러 올라가면 세부 경로가 A, E, C임을 알 수 있다.
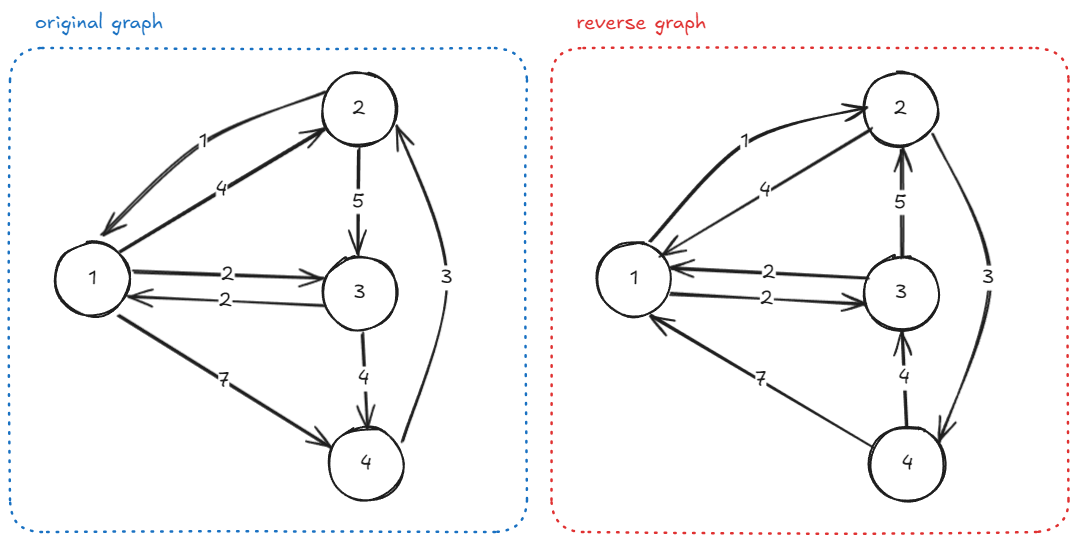
5. 🚀 응용
모든 노드가 출발 노드가 되는 경우
주어지는 그래프의 방향을 반대로 뒤집고 도착해야 할 노드를 출발 노드로 설정하면 구해진 값들이 각 노드로부터 도착해야 할 노드까지의 최소 비용이 된다.
6. 📝 코드 구현
우선순위 큐를 활용한 구현과 배열을 활용한 구현을 모두 소개한다. 배열을 활용한 구현은 시간 복잡도가 더 높아 노드 수가 많아지면 성능이 급격히 저하된다.
- 우선순위 큐 구현과 배열 구현의 주요 차이점:
- 우선순위 큐 대신 배열 사용
- 방문 여부를 체크하는 visited 배열 추가
- 매 반복마다 최소 거리를 가진 노드를 찾기 위해 모든 노드를 검사
- 시간 복잡도는 $O(V^2)$로 우선순위 큐 구현($O(E \log V)$)보다 느림
0
/ \
1---2 가중치 예시:
/|\ 0->1: 4, 0->2: 2, 1->2: 3
3 4 5 1->3: 1, 1->4: 5, 1->5: 2
5.1. C++
이 코드는 우선순위 큐를 사용한 구현이며, 직관적이지 않을 수 있다.
#include <iostream>
#include <vector>
#include <queue>
#include <limits>
void dijkstra(int start, const std::vector<std::vector<std::pair<int, int>>>& graph) {
int n = graph.size();
std::vector<int> dist(n, std::numeric_limits<int>::max());
std::vector<int> prev(n, -1); // 경로 추적을 위한 배열
// 우선순위 큐 초기화 (거리, 노드)
std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<>> pq;
// 시작 노드 초기화
dist[start] = 0;
pq.push({start, dist[start]});
while (!pq.empty()) {
auto [current_node, current_dist] = pq.top();
pq.pop();
// 현재 거리가 이미 알고 있는 거리보다 크면 스킵
if (current_dist > dist[current_node]) continue;
// 인접 노드들을 확인
for (const auto& [next_node, next_dist] : graph[current_node]) {
// 더 짧은 경로를 발견한 경우
if (current_dist + next_dist < dist[next_node]) {
dist[next_node] = current_dist + next_dist;
prev[next_node] = current_node;
pq.push({next_node, dist[next_node]});
}
}
}
// 결과 출력
for (int i = 0; i < n; i++) {
std::cout << "Node " << i << ": ";
if (dist[i] == std::numeric_limits<int>::max())
std::cout << "INF" << std::endl;
else
std::cout << dist[i] << std::endl;
}
}
int main() {
// 그래프 정의 (노드, {연결된 노드, 가중치})
std::vector<std::vector<std::pair<int, int>>> graph = {
{{1, 4}, {2, 2}}, // 0번 노드
{{0, 4}, {2, 3}, {3, 1}, {4, 5}, {5, 2}}, // 1번 노드
{{0, 2}, {1, 3}}, // 2번 노드
{{1, 1}}, // 3번 노드
{{1, 5}}, // 4번 노드
{{1, 2}} // 5번 노드
};
dijkstra(0, graph); // 시작 노드: 0
return 0;
}
5.2. Python
이 코드는 우선순위 큐를 사용한 구현이며, 직관적이지 않을 수 있다.
import heapq
from typing import List, Dict, Set
from collections import defaultdict
def dijkstra(start: int, graph: Dict[int, List[tuple]]) -> Dict[int, int]:
# 거리 저장 딕셔너리 초기화
distances = {node: float('inf') for node in graph}
distances[start] = 0
# 우선순위 큐 초기화 (거리, 노드)
pq = [(0, start)]
# 경로 추적을 위한 딕셔너리
previous = {node: None for node in graph}
while pq:
current_dist, current = heapq.heappop(pq)
# 현재 거리가 이미 알고 있는 거리보다 크면 스킵
if current_dist > distances[current]:
continue
# 인접 노드들을 확인
for next_node, weight in graph[current]:
new_dist = distances[current] + weight
# 더 짧은 경로를 발견한 경우
if new_dist < distances[next_node]:
distances[next_node] = new_dist
previous[next_node] = current
heapq.heappush(pq, (new_dist, next_node))
# 결과 출력
for node in graph:
print(f"Node {node}: {distances[node] if distances[node] != float('inf') else 'INF'}")
return distances
if __name__ == "__main__":
# 그래프 정의 (노드: [(연결된 노드, 가중치)])
graph = {
0: [(1, 4), (2, 2)],
1: [(0, 4), (2, 3), (3, 1), (4, 5), (5, 2)],
2: [(0, 2), (1, 3)],
3: [(1, 1)],
4: [(1, 5)],
5: [(1, 2)]
}
dijkstra(0, graph) # 시작 노드: 0
5.3. 배열을 사용한 구현
C++
#include <iostream>
#include <vector>
#include <limits>
void dijkstra_array(int start, const std::vector<std::vector<std::pair<int, int>>>& graph) {
int n = graph.size();
std::vector<int> dist(n, std::numeric_limits<int>::max());
std::vector<bool> visited(n, false);
std::vector<int> prev(n, -1); // 경로 추적을 위한 배열
// 시작 노드 초기화
dist[start] = 0;
// 모든 노드에 대해 반복
for (int i = 0; i < n; i++) {
// 방문하지 않은 노드 중 최소 거리를 가진 노드 찾기
int min_dist = std::numeric_limits<int>::max();
int current = -1;
for (int j = 0; j < n; j++) {
if (!visited[j] && dist[j] < min_dist) {
min_dist = dist[j];
current = j;
}
}
if (current == -1) break; // 더 이상 방문할 수 있는 노드가 없음
// 현재 노드를 방문 처리
visited[current] = true;
// 인접 노드들의 거리 갱신
for (const auto& [next, weight] : graph[current]) {
if (!visited[next]) {
int new_dist = dist[current] + weight;
if (new_dist < dist[next]) {
dist[next] = new_dist;
prev[next] = current;
}
}
}
}
// 결과 출력
for (int i = 0; i < n; i++) {
std::cout << "Node " << i << ": ";
if (dist[i] == std::numeric_limits<int>::max())
std::cout << "INF" << std::endl;
else
std::cout << dist[i] << std::endl;
}
}
Python
def dijkstra_array(start: int, graph: Dict[int, List[tuple]]) -> Dict[int, int]:
# 초기화
n = len(graph)
distances = {node: float('inf') for node in graph}
distances[start] = 0
visited = {node: False for node in graph}
previous = {node: None for node in graph}
for _ in range(n):
# 방문하지 않은 노드 중 최소 거리를 가진 노드 찾기
min_dist = float('inf')
current = None
for node in graph:
if not visited[node] and distances[node] < min_dist:
min_dist = distances[node]
current = node
if current is None: # 더 이상 방문할 수 있는 노드가 없음
break
# 현재 노드를 방문 처리
visited[current] = True
# 인접 노드들의 거리 갱신
for next_node, weight in graph[current]:
if not visited[next_node]:
new_dist = distances[current] + weight
if new_dist < distances[next_node]:
distances[next_node] = new_dist
previous[next_node] = current
# 결과 출력
for node in graph:
print(f"Node {node}: {distances[node] if distances[node] != float('inf') else 'INF'}")
return distances