[알고리즘] 깊이 우선 탐색(DFS) 구현(C++, Python)
카테고리: Algorithm Theory
1. 🔍 깊이 우선 탐색(DFS, Depth-First Search)
시작 노드부터 탐색을 시작하여 간선을 따라 최대 깊이 노드까지 이동하며 차례대로 방문한다. 최대 깊이 노드까지 방문한 다음에는 이전에 방문한 노드를 거슬러 올라가며 해당 노드와 연결된 노드 중 방문하지 않은 노드로 다시 최대 깊이까지 차례대로 방문한다.
2. 💡 DFS 알고리즘
- 탐색을 하려면 시작 노드를 정하고 스택에 시작 노드를 푸시한다. 스택에 있는 노드는 아직 방문하지 않았지만 방문할 예정인 노드이다. 이후 다음 과정을 반복한다.
- 스택이 비었는지 확인한다. 스택이 비었다는 건 방문할 수 있는 모든 노드를 방문했음을 의미한다. 따라서 스택이 비었으면 탐색을 종료한다.
- 스택에서 노드를 팝한다. 팝한 원소는 최근에 스택에 푸시한 노드이다.
- 팝한 노드의 방문 여부를 확인한다. 아직 방문하지 않았다면 노드를 방문 처리한다.
- 방문한 노드와 인접한 모든 노드를 확인한다. 그중에서 아직 방문하지 않은 노드를 스택에 푸시한다. 스택은 LIFO 구조이므로 방문 순서를 오름차순으로 고려한다면 역순으로 노드를 푸시해야 한다.
3. ⚠️ 고려 사항
- 탐색할 노드가 없을 때까지 간선을 타고 내려갈 수 있어야 한다.
- 가장 최근에 방문한 노드를 알아야 한다.
- 이미 방문한 노드인지 확인할 수 있어야 한다.
4. 🛠️ 스택을 활용한 DFS
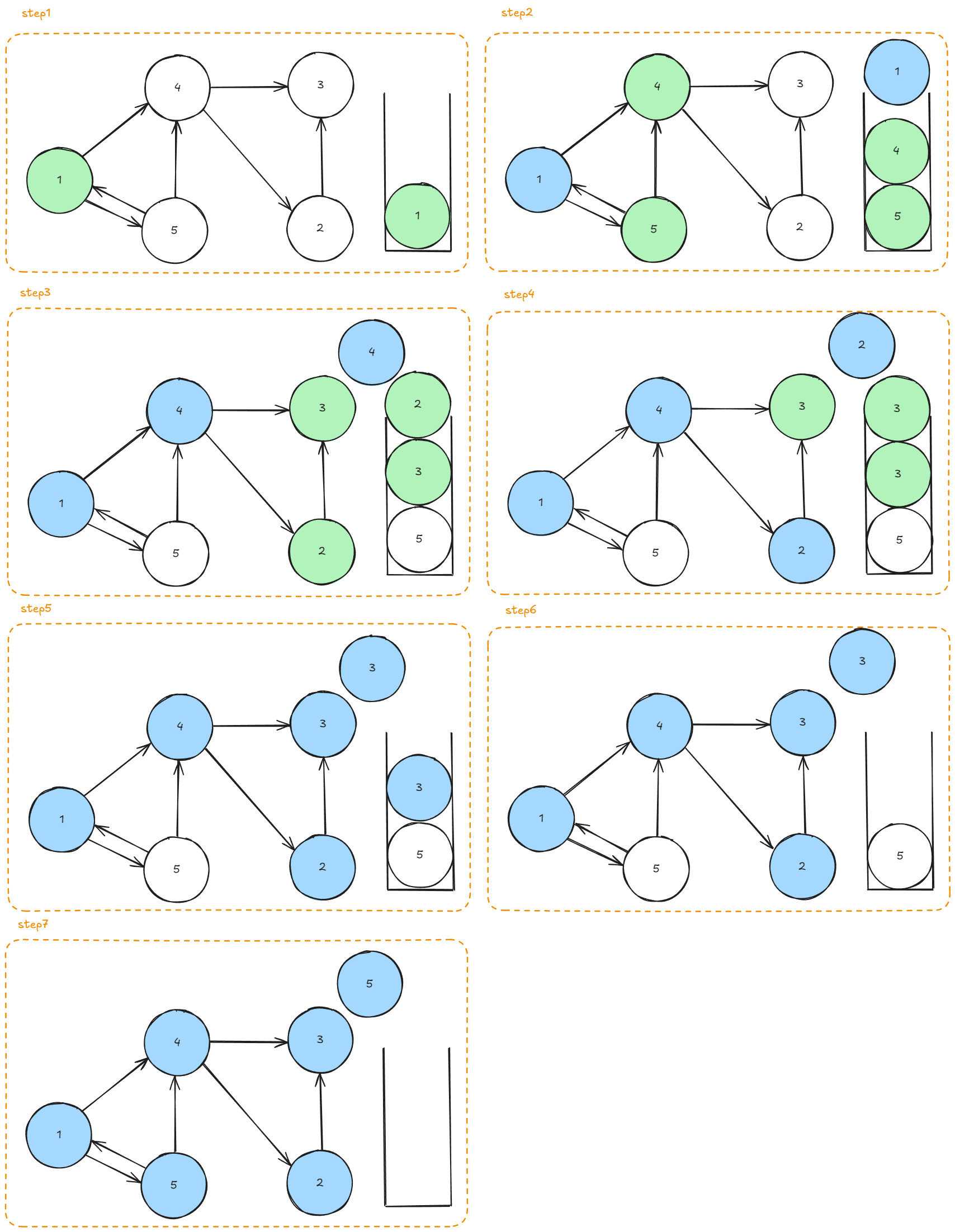
- 스택에 푸시한 노드는 초록색, 방문한 노드는 하늘색으로 색칠한다.
- 1단계: 아직 1은 방문하지 않았고 방문할 예정이기만 하므로 그래프는 푸시한 노드만 색칠되어 있다.
- 2단계: 1을 팝한 후에 1이 방문한 상태인지 확인한다. 1은 아직 방문하지 않은 노드이므로 방문 처리를 한다(하늘색으로 색칠). 방문 처리를 한 후에는 1과 인접하면서 방문하지 않은 노드 5, 4를 푸시하여 이후에 방문 처리할 수 있도록 한다(순서는 상관 없다. 결국 모두 탐색하게 된다.).
- 3단계: 스택에서 4를 팝한 다음, 4가 방문한 상태인지 확인한다. 4는 아직 방문하지 않았으므로 방문 처리한다. 그런 다음 4와 인접한 3, 2를 푸시한다.
- 4단계: 2를 팝한다. 2는 방문하지 않았으므로 2를 방문 처리한다. 그런 다음 2와 인접하면서 방문하지 않은 노드 3을 푸시한다.
- 5단계: 3을 팝하고 방문 처리한다. 3과 인접하면서 방문하지 않은 노드가 없으니 아무것도 푸시하지 않는다.
- 6단계: 또 다시 3을 팝했지만 이미 방문 처리를 했으므로 아무 작업도 하지 않는다.
- 7단계: 5를 팝하고 방문 처리한다. 스택이 비었으므로 작업이 끝난다.
5. 📞 재귀 함수를 활용한 깊이 우선 탐색
- 재귀 함수를 호출할 때마다 시스템 스택에 호출한 함수가 쌓이므로 깊이 우선 탐색에 활용할 수 있다.
- 호출할 함수는
dfs()라 선언하고dfs(N)을 호출하면 다음 동작을 하도록 구현한다.dfs(N): N번 노드를 방문 처리하고 N번 노드와 인접한 노드 중 아직 방문하지 않은 노드를 탐색한다.
6. 📝 코드 구현
0
/ \
1 2
/ \
3 4
6.1. C++
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
void dfs(int node, vector<bool>& visited, const vector<vector<int>>& graph) {
// 현재 노드를 방문 처리
visited[node] = true;
cout << node << " ";
// 인접한 노드 탐색
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
dfs(neighbor, visited, graph);
}
}
}
int main() {
// 그래프 정의 (예: 0-1-2-3-4)
vector<vector<int>> graph = {
{1, 2}, // 0
{0, 3, 4}, // 1
{0}, // 2
{1}, // 3
{1} // 4
};
vector<bool> visited(graph.size(), false);
dfs(0, visited, graph); // 시작 노드: 0
return 0;
}
6.2. Python
def dfs(node, visited, graph):
# 현재 노드를 방문 처리
visited[node] = True
print(node, end=" ")
# 인접한 노드 탐색
for neighbor in graph[node]:
if not visited[neighbor]:
dfs(neighbor, visited, graph)
if __name__ == "__main__":
# 그래프 정의 (예: 0-1-2-3-4)
graph = {
0: [1, 2],
1: [0, 3, 4],
2: [0],
3: [1],
4: [1]
}
visited = [False] * len(graph)
dfs(0, visited, graph) # 시작 노드: 0