[알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm) 구현(C++, Python)

1. 🔍 벨만-포드 알고리즘(Bellman-Ford Algorithm)

다익스트라 알고리즘과 마찬가지로 노드에서 노드까지의 최소 비용을 구한다는 점에서 같지만, 벨만-포드 알고리즘은 매 단계마다 모든 간선의 가중치를 다시 확인하여 최소 비용을 갱신하므로 음의 가중치를 가지는 그래프에서도 최단 경로를 구할 수 있다.

2. 💡 벨만-포드 알고리즘 동작 과정

1. 시작 노드를 설정한 다음 시작 노드의 최소 비용은 0, 나머지 노드는 INF로 초기화한다. 이후 최소 비용을 갱신할 때 직전 노드도 갱신한다.
2. 노드 개수 - 1만큼 다음 연산을 반복한다.
   1. 시작 노드에서 갈 수 있는 각 노드에 대하여 전체 노드 각각을 거쳐갈 때 현재까지 구한 최소 비용보다 더 적은 최소 비용이 있는지 확인하여 갱신한다. 최소 비용을 갱신할 때, V의 직전 노드 값도 같이 갱신한다.
3. 과정 2-1을 마지막으로 한 번 더 수행하여 갱신되는 최소 비용이 있는지 확인한다. 만약 있다면 음의 순환이 있음을 의미한다.

3. ⚠️ 고려 사항

• 음의 순환이 존재하면 다익스트라 알고리즘과 마찬가지로 최소 비용을 구할 수 없다.

4. 🎨 그림과 함께 알고리즘 생각해보기

예시 그림과 함께 알고리즘을 생각해보자.

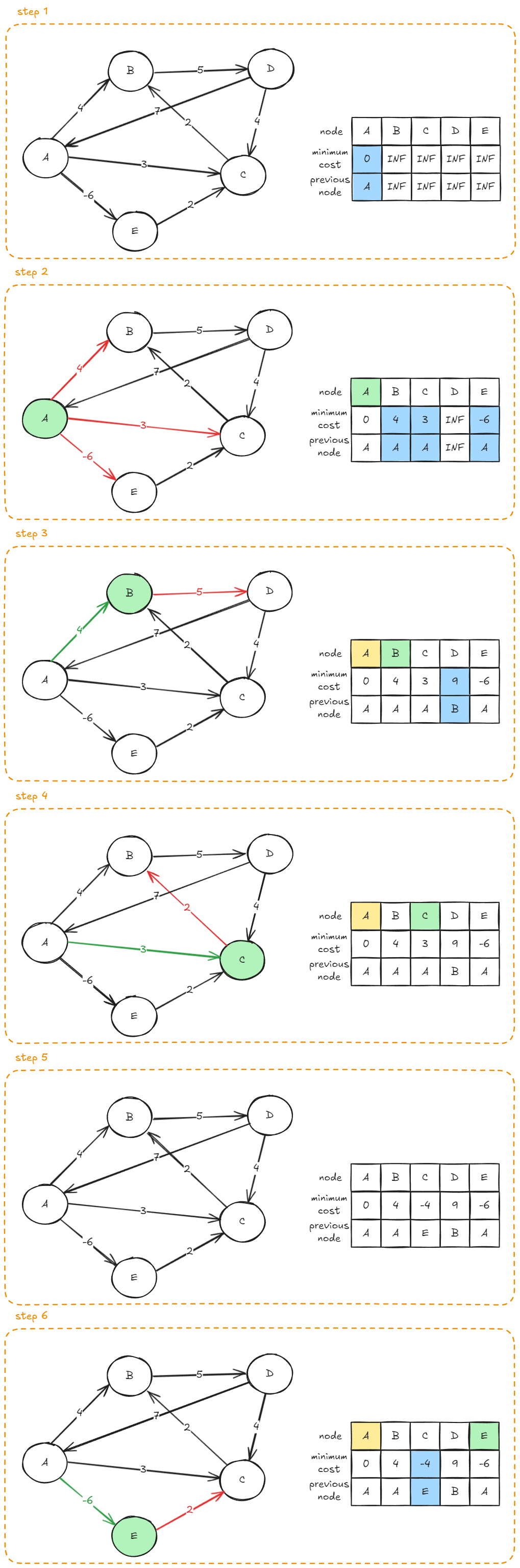
• 1단계: 우선 시작 노드를 A로 정하고 최소 비용을 0, 직전 노드를 A, 나머지 노드는 INF로 초기화한다.
• 2단계: 노드 A에서 A를 거쳐 각 노드 B, C, D, E까지 가는 비용 중 현재까지 구한 최소 비용보다 적은 값이 있는지 확인하고 현재까지 구한 최소 비용보다 비용이 적다면 갱신한다. 간선이 없는 경우는 INF로 계산한다.
  • 노드 A 기준으로 보면 다음과 같다.
    • A 최소 비용: 갱신하지 않음(0 + 0)
    • B 최소 비용: INF에서 4로 갱신(0 + 4)
    • C 최소 비용: INF에서 3으로 갱신(0 + 3)
    • D 최소 비용: 갱신하지 않음(0 + INF)
    • E 최소 비용: INF에서 -6으로 갱신(0 + -6)
• 3단계: 노드 A에서 B를 거쳐 각 노드까지 가는 최소 비용도 갱신한다.
  • A 최소 비용: 갱신하지 않음(4 + INF)
  • B 최소 비용: 갱신하지 않음(4 + 0)
  • C 최소 비용: 갱신하지 않음(4 + INF)
  • D 최소 비용: INF에서 9로 갱신(4 + 5)
  • E 최소 비용: 갱신하지 않음(4 + INF)
• 4단계: 노드 A에서 C를 거쳐 각 노드까지 가는 최소 비용도 갱신한다.
  • A 최소 비용: 갱신하지 않음(3 + INF)
  • B 최소 비용: 갱신하지 않음(3 + 2)
  • C 최소 비용: 갱신하지 않음(3 + 0)
  • D 최소 비용: 갱신하지 않음(3 + INF)
  • E 최소 비용: 갱신하지 않음(3 + INF)
• 5단계: 노드 A에서 D를 거쳐가는 방법은 없으므로 갱신하지 않는다.
• 6단계: 노드 A에서 E를 거쳐 각 노드까지 가는 최소 비용도 갱신한다.
  • A 최소 비용: 갱신하지 않음(-6 + INF)
  • B 최소 비용: 갱신하지 않음(-6 + INF)
  • C 최소 비용: 갱신하지 않음(-6 + 2)
  • D 최소 비용: 갱신하지 않음(-6 + INF)
  • E 최소 비용: 갱신하지 않음(-6 + INF)
• 7단계: 이제 1단계에서 6단계를 노드 개수 - 1번 반복한다.

5. 벨만-포드 알고리즘에서의 반복

5.1. 노드 개수 - 1번 반복

매 반복마다 모든 간선을 확인하여 최소 비용을 갱신한다. 반복할 때마다 최단 경로가 1개씩 확정된다.

5.2. 음수 사이클 체크

노드 개수 - 1번 반복 후 한 번 더 반복을 한다. 마지막 반복에서 최소 비용이 갱신되는 경우 음수 사이클이 존재한다는 의미이다.

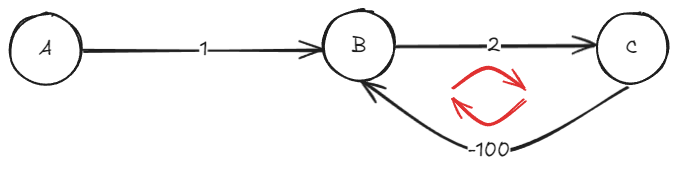
• 아래 그림처럼 계속 순환했을 때 최단 경로가 계속 갱신된다면 실질적으로 최단 경로는 구할 수 없게 된다.
  • 이를 찾으려면 정점 개수만큼은 반복 연산해야 체크가 가능하다.
• 그래프에 음의 순환이 있으면 어떤 알고리즘도 최단 경로를 구할 수 없다.
  • 벨만 포드 알고리즘은 이런 음의 순환도 찾아낼 수 있는 알고리즘이다.

6. 📝 코드 구현

    0
   / \
  1---2    가중치 예시:
 /|\     0->1: 4, 0->2: 2, 1->2: 3
3 4 5    1->3: 1, 1->4: 5, 1->5: 2

6.1. C++

#include <iostream>
#include <vector>
#include <limits>

void bellman_ford(size_t start, const std::vector<std::vector<std::pair<size_t, long long>>>& graph, size_t n) {
    std::vector<long long> dist(n, std::numeric_limits<long long>::max());
    dist[start] = 0;

    // n-1번 반복
    for (size_t i = 1; i < n; i++) {
        for (size_t u = 0; u < n; u++) {
            for (auto [v, weight] : graph[u]) {
                if (dist[u] != std::numeric_limits<long long>::max() && dist[u] + weight < dist[v]) {
                    dist[v] = dist[u] + weight;
                }
            }
        }
    }

    // 음수 사이클 체크
    for (size_t u = 0; u < n; u++) {
        for (auto [v, weight] : graph[u]) {
            if (dist[u] != std::numeric_limits<long long>::max() && dist[u] + weight < dist[v]) {
                std::cout << "Negative weight cycle detected!\n";
                return;
            }
        }
    }

    // 결과 출력
    for (size_t i = 0; i < n; i++) {
        std::cout << "Node " << i << ": ";
        if (dist[i] == std::numeric_limits<long long>::max())
            std::cout << "INF\n";
        else
            std::cout << dist[i] << "\n";
    }
}

int main() {
    size_t v = 6; // 노드 수
    std::vector<std::vector<std::pair<size_t, long long>>> graph(v);

    // 그래프 정의 (노드, {연결된 노드, 가중치})
    graph[0] = {{1, 4}, {2, 2}};
    graph[1] = {{2, 3}, {3, 1}, {4, 5}, {5, 2}};
    graph[2] = {{1, 3}};
    graph[3] = {{1, 1}};
    graph[4] = {{1, 5}};
    graph[5] = {{1, 2}};

    bellman_ford(0, graph, v);  // 시작 노드: 0
    return 0;
}

6.2. Python

import heapq
from typing import List, Dict, Set
from collections import defaultdict

def bellman_ford(start: int, graph: Dict[int, List[tuple]], V: int) -> Dict[int, int]:
    # 거리 저장 딕셔너리 초기화
    distances = {node: float('inf') for node in range(V)}
    distances[start] = 0

    # V-1번 반복
    for _ in range(V - 1):
        for u in range(V):
            for next_node, weight in graph[u]:
                if distances[u] != float('inf') and distances[u] + weight < distances[next_node]:
                    distances[next_node] = distances[u] + weight

    # 음수 사이클 체크
    for u in range(V):
        for next_node, weight in graph[u]:
            if distances[u] != float('inf') and distances[u] + weight < distances[next_node]:
                print("Negative weight cycle detected!")
                return

    # 결과 출력
    for node in range(V):
        print(f"Node {node}: {distances[node] if distances[node] != float('inf') else 'INF'}")

    return distances

if __name__ == "__main__":
    V = 6  # 노드 수
    # 그래프 정의 (노드: [(연결된 노드, 가중치)])
    graph = {
        0: [(1, 4), (2, 2)],
        1: [(2, 3), (3, 1), (4, 5), (5, 2)],
        2: [(1, 3)],
        3: [(1, 1)],
        4: [(1, 5)],
        5: [(1, 2)]
    }

    bellman_ford(0, graph, V)  # 시작 노드: 0

Algorithm Theory 카테고리 내 다른 글 보러가기