[자료구조] 그래프 기본 개념 정리
카테고리: Algorithm Theory
태그: algorithm coding test data structure graph implementation graph
1. 🔍 그래프(Graph)의 개념
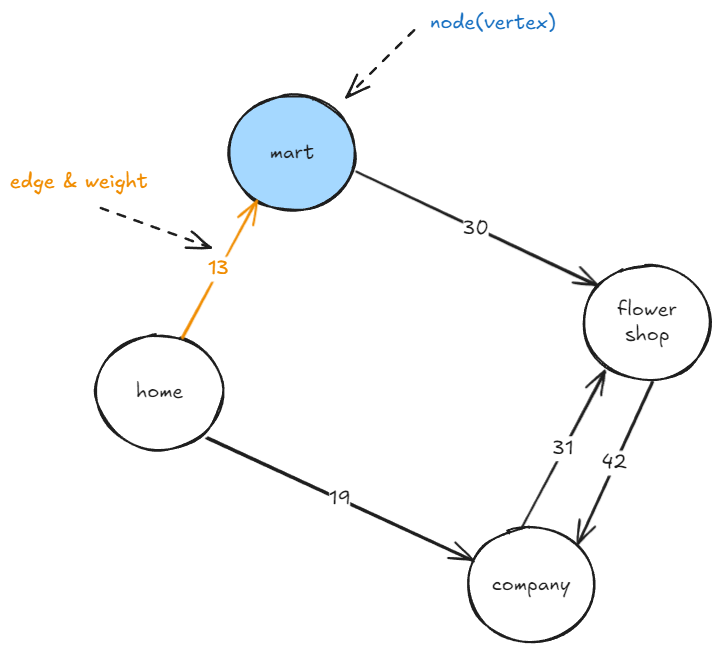
그래프는 노드(vertex)와 간선(edge)을 이용한 비선형 데이터 구조이다.
- 보통 그래프는 데이터 간의 관계를 표현하는 데 사용하며, 데이터를 노드로, 노드 간의 관계나 흐름을 간선으로 표현한다.
- 간선은 방향이 있을 수도 있고 없을 수도 있다.
- 만약 관계나 흐름에서 정도를 표현할 필요가 있다면 가중치라는 개념을 추가하여 표현한다.
그래프 용어 정리
- 그래프는 방향성, 가중치, 순환 특성에 따라 종류를 구분할 수 있다.
흐름을 표현하는 방향성
- 간선은 방향을 가질 수도 있고 없을 수도 있다.
- 방향이 있는 간선을 포함하면 방향 그래프(directed graph), 방향이 없는 간선을 포함하면 무방향 그래프(undirected graph) 라고 한다.
흐름의 정도를 표현하는 가중치
- 어떤 데이터는 흐름의 방향뿐 아니라 양도 중요할 수 있다.
- 그 정도를 간선에 표현할 때 이를 가중치라고 한다.
- 가중치가 있는 그래프를 가중치 그래프(weight graph) 라고 한다.
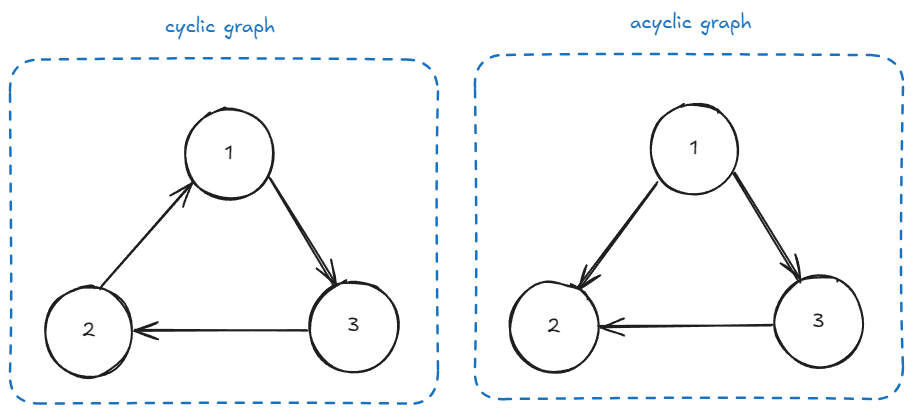
시작과 끝의 연결 여부를 보는 순환
- 순환은 특정 노드에서 시작해 간선을 따라 다시 돌아오는 경로가 있는 것을 말한다.
- 순환이 존재하는 그래프를 순환 그래프(cyclic graph), 순환이 존재하지 않는 그래프를 비순환 그래프(acyclic graph) 라고 한다.
2. ✨ 그래프 구현 방법
그래프의 구현 방식에는 인접 행렬(adjacency matrix)과 인접 리스트(adjacency list)가 있다.
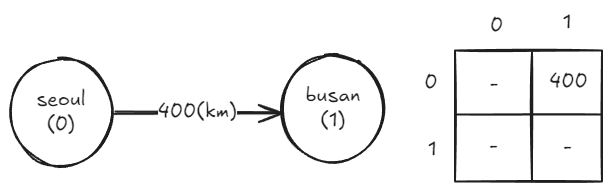
인접 행렬로 그래프 표현하기
- 배열을 활용하여 구현하는 경우가 많다.
- 배열의 인덱스는 노드
- 배열의 값은 노드의 가중치
- 인덱스 세로 방향을 출발 노드
- 인덱스 가로 방향을 도착 노드
- 값이 들어가지 않는 경우 굉장히 큰 값을 넣거나 -1로 채운다.
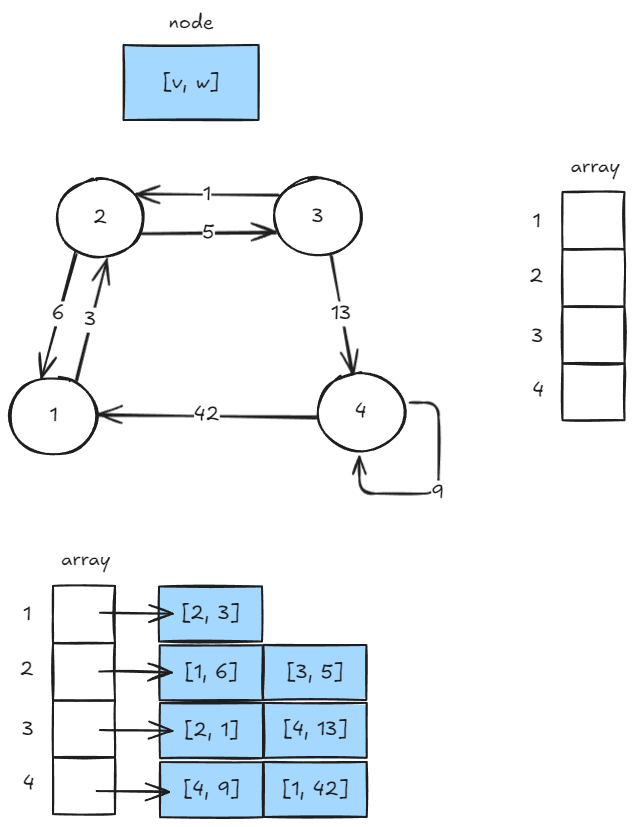
인접 리스트로 그래프 표현하기
- 인접 리스트로 그래프를 표현하려면 적절한 노드를 정의해야 한다.
- 정점(v)와 가중치(w)를 묶어 관리한다.
- 노드 개수만큼 배열을 준비한다.
- 배열의 인덱스는 각 시작 노드를 의미하며 배열의 값에는 해당 노드를 시작 노드로 하는 노드들을 추가한다.
구현 방법에 대한 장단점 비교하기
어느 한쪽이 매우 뛰어나거나 부족하지 않다. 모두 장단점이 있다. 간선의 수가 $E$이고 정점의 수가 $V$이다.
| 공간 복잡도 | 특정 정점의 간선을 찾는 경우 시간 복잡도 | 그래프의 모든 간선을 찾는 경우 시간 복잡도 | |
|---|---|---|---|
| 인접 행렬 | $O(V^2)$ | $O(1)$ | $O(V^2)$ |
| 인접 리스트 | $O(V+E)$ | $O(E)$ (대부분의 연산 횟수는 $E/V$) | $O(V+E)$ |
인접 행렬의 장단점
- 장점
- 간선의 정보를 확인할 때 시간 복잡도가 $O(1)$이다. 인덱스 접근으로 바로 확인 가능하다.
- 구현 난이도가 낮다.
- 단점
- 인접 행렬로 희소 그래프(간선 수가 매우 적은 그래프)를 표현하는 경우, 데이터가 많이 없는데 메모리만 잡아먹고 있을 수 있다.
인접 리스트의 장단점
- 장점
- 메모리를 아낄 수 있다.
- 단점
- 최악의 경우 각 노드에서 모든 노드에 간선이 연결되어 있을 때 효율이 떨어진다.
- 구현 난이도가 높다.
3. 🔄 그래프 탐색
그래프에서 경로를 찾을 때 경로를 찾는 방법은 크게 2가지가 있다.
- 깊이 우선 탐색(depth-first search, DFS): 더 이상 탐색할 노드가 없을 때까지 일단 간다. 가다가 더 이상 탐색할 노드가 없다면 최근에 방문했던 노드로 되돌아간 다음 가지 않은 노드를 방문한다.
- 너비 우선 탐색(breadth-first search, BFS): 현재 위치에서 가장 가까운 노드부터 모두 방문하고 다음 노드로 넘어간다. 그 노드에 다시 가장 가까운 노드부터 모두 방문한다.
깊이 우선 탐색과 너비 우선 탐색 비교
깊이 우선 탐색은 깊게 탐색 후 되돌아오는 특성이 있고, 너비 우선 탐색은 시작 노드에서 인접한 노드부터 방문하는 특성을 가진다.
깊이 탐색 후 되돌아오는 깊이 우선 탐색 (DFS)
- 가장 깊은 곳을 우선하여 탐색하고, 더 이상 탐색할 수 없으면 백트래킹하여 최근 방문 노드부터 다시 탐색을 진행한다.
- 활용 사례:
- 백트래킹이 필요한 문제 (예: N-Queens, 순열/조합 생성)
- 그래프의 사이클 감지
- 위상 정렬
- 연결된 컴포넌트 찾기
- 장점:
- 메모리 사용량이 적음 (현재 경로상의 노드들만 저장)
- 목표 노드가 깊은 단계에 있을 때 유리
- 구현이 비교적 간단함
- 단점:
- 최단 경로를 보장하지 않음
- 무한 깊이의 경우 빠져나오지 못할 수 있음
최단 경로를 보장하는 너비 우선 탐색 (BFS)
- 시작 노드로부터 가까운 노드들을 우선적으로 방문하여 최단 경로를 보장한다.
- 활용 사례:
- 최단 경로 찾기 문제
- 미로 탐색
- 네트워크 홉(hop) 분석
- 소셜 네트워크에서 친구 추천
- 장점:
- 최단 경로 보장
- 레벨 단위의 탐색이 필요할 때 유리
- 무한 루프에 빠질 위험이 적음
- 단점:
- 메모리 사용량이 많음 (동일 레벨의 모든 노드를 저장)
- 구현이 DFS보다 복잡할 수 있음
코딩 테스트 팁
- DFS 선택 시기:
- 모든 경우를 탐색해야 할 때
- 경로의 특징을 저장해야 할 때
- 검색 대상이 깊은 단계에 있을 것으로 예상될 때
- BFS 선택 시기:
- 최단 거리/경로를 구해야 할 때
- 검색 대상이 시작 지점에서 가까울 것으로 예상될 때
- 레벨 단위로 탐색해야 할 때